One of the big frustrations I have when discussing grades with others (whether that be teachers, students, or parents) is that the argument frequently comes down to an unfounded faith in percent. The argument goes something like this:
- Well, we have to have grades. (I disagree.)
- You have to set a cut off somewhere. (Why?)
- This is the percent the student got, math never lies, so therefore this grade is accurate and fair. (Oh really?)
It's toward the end of the semester and a student has an 89.5% in a class. They turn in a review guide and get a 20 out of 20 on it. What happens to their overall grade? Does it go up? Stay the same? Or go down?
The vast majority of folks say it will go up. The answer, of course, is it depends. In this particular case, the grade goes down. Yes, a student who has an 89.5% in the class turns in their review guide assignment like a good student should and gets a 100% on it, yet their grade still goes down.
How is that possible? Well, this teacher weights their grades by category. This assignment falls in the Homework Category which gets a weight of 10%. Because this teacher previously offered some extra credit (which is a whole different blog rant), the student's percentage in the homework category before the review guide was turned in was 105.7%. After turning in her correctly done review guide, her percent in that category drops from a 105.7 to a 105, and her overall grade drops from an 89.5 to an 89.4 (which, for many teachers, is from an A to a B - most teachers in my building will "round up" an 89.5).
In effect, the student is penalized for turning in a perfect assignment. What grade should they get?
Recent Example #2
At the end of the semester a student has an 89.1% in a class out of a total of 2,389 points. What happens to their overall grade if they scored 1 point higher on one single assignment earlier in the semester?
Again, of course, it depends. In this particular case, it would raise their overall grade to 89.815% which, again for most teachers in my building, is probably the difference between a B and an A. Some of you will doubt that 1 point out of 2,389 can raise their grade from an 89.1 to an 89.815, but it can. This teacher weights categories as well, and one of their categories is titled Homework Checks and is worth 10% of the overall grade. Here is the student's scores in that category:
See that Slope Quiz on October 31st that the student scored a 7 out of 8 on? If they had received an 8 out of 8, their category percentage rises to 100%, which increases their overall percentage in the class by 0.715%, from 89.1 to 89.815.
One point, on one quiz, on one day. What grade should they get?
Recent Example #3
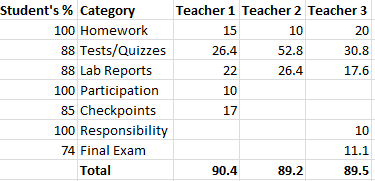
Here's a student's percentages in different categories for a particular class:
Homework: 100%
Tests & Quizzes: 88%
Lab Reports: 88%
Participation: 100%
Checkpoints: 85%
Responsibility: 100%
Final Exam: 74%
Well, we could have a long and valuable philosophical discussion about this, but the point of this example is that this student could get two different grades in the same class at my school. How? It depends on what teacher they have and how that teacher weights their categories. Here's what it looks like for three teachers of this class in my building:
And here's what that translates to for the student's percentages in each category:
These teachers all teach the same class. Students are randomly scheduled into their class by the computer. This student could have performed exactly the same and, in one class, received an 89.2% (a B), an 89.5% (probably an A, but possibly a B), or 90.4% (an A), because the teachers choose to weight the categories differently. Oh, and there are two other teachers of this section that grade on total points, so the student would have yet another percentage that we can't determine from this information.
The same student, in the same class, with the same curriculum, at the same school. What grade should they get?
All three of these examples are real, from my school, from the end of last semester, although I did manipulate the overall percentages for effect (but the assignments and student scores on examples 1 and 2, and the teacher weights on all three examples, are real).
So, even if you believe grades are worthwhile (or if you don't believe grades are worthwhile but you have to give them anyway), I would at least ask that you spend a little more time thinking about them. Your computer grade book is mathematically accurate; it computes exactly what you tell it to compute. But that doesn't mean it makes sense. You are the professional, and if you give a grade to a student you should come up with a more thoughtful way to assign that grade than simply relying on a percentage.


Grades are hypothetical constructs, not unlike our judgement of student learning. The reality is we are just making this stuff up as we go, using what the students choose to show us to 'prove' their learning.
ReplyDeleteYep, But other than that, they're perfect!
DeleteYou may want to check out a wonderful group on Facebook, Assessment 3.0. Group is all about replacing grades. Wonderful conversations.
ReplyDeleteLooks like you can find Assessment 3.0 at https://www.facebook.com/pages/Assessment-30/311928245661221 if you're interested.
DeleteI totally agree that it is important to be thoughtful when assigning grades. How do you address, assuming you are giving grades, the notion of neutrality and fairness? Aren't grades the way we as teachers can treat everyone equally? Thoughtfulness towards the grade is a gray area. I'm all for gray areas in life, but it gets tricky when parents become involved, and transcripts and college applications.
ReplyDeleteAssuming we have to give grades, one student's grade has nothing to do with another student's grade. The grade we give a student should be representative of what they know - it has nothing to do with what any other student knows. If grades have to be given, then standards-based-grades (sbg) is the best way I've seen.
DeleteAll of these counter-intuitive results from weighted grading are the primary reason I'm a huge opponent of that form of grading. While weighted grading allows much more flexibility in creating assignments on the fly, it's far more complex for students and produces the kind of nonsense we saw in the examples in your post.
ReplyDeleteI think a skilled teacher can use an unweighted grading system and achieve nearly as much flexibility with the additional advantage of a more fair and transparent result for students.
(Although I'm with a lot of people who think that evaluating education with grades in the first place is pretty nonsensical. If we're going to be nonsensical, we should at least make the system easy to use.)
I wonder if grades aren't the issue but instead the false accuracy of percents. We are lead to believe that because we can calculate a percent to any number of decimal places that it is accurate to that same number of decimals. Part of this is due the issue of separating accuracy and precision as to related but different things.
ReplyDeleteMeasuring a student's ability in any capacity is a very squishy measurement. It's not the kind of thing we can truly measure very accurately. So for all of your examples, I would argue, the point is moot. They are all essentially the same grade. Humans focus too much on those numbers as meaningful (significant digits for you science folk) but they are not (for many reasons).
I usually ask teachers to articulate the characteristics of a student who has 81% vs 82% in their class and they cannot. But you could probably articulate the difference between a student who has 85% and 75%.
And although your examples of different marking schemes are real (though I am surprised there wouldn't be some sort of consistency within a school - at least for similar subjects), the other issue is that of how we actually grade. It is pretty easy to grade work that is perfect or near perfect and to grade work that is completely wrong. But for work that is in the middle, it is hard to get a consistent grade (especially if you ask different teachers). I do an exercise with teachers where I give them a fairly complex piece of student math work (requires multiple steps) that has an incorrect final answer and ask them to grade it using their own grading scale. Invariably I get marks ranging from 20% -70% for the same piece of work!
So to think that we can somehow, with confidence, give a student a percentage grade and have it be accurate to the stated percent is probably a pipe dream.
Absolutely, the sum of the many, many, many decisions (often arbitrary, or at least not completely thought out in the context of this discussion) that teachers make during a grading period far outweighs any kind of "precision."
DeleteI think the false accuracy of percents is certainly an issue within the concept of grades (that was the point of using those specific examples), but I think grades are still the issue. I don't think there's any way to have a "grade" assigned that doesn't undermine what we are trying to do with students.
Very interesting! As a future educator I have never really had give grades yet. But you post really makes me think about how I will grade in my future classroom.
ReplyDeleteHi Karl,
ReplyDeleteI am an AHS alumnus, with many other connections to learning, coaching, education, technology, etc. I got to this entry through your Goals Gone Wild post of 01 May 2016 (http://thefischbowl.blogspot.com/2016/05/goals-gone-wild.html), but I had to comment here before returning. My comment there will be more full-bodied.
Without as much thought as you and others have given, I am probably in agreement with your perspective on grading. I might describe that technically, the categorization that you've identified in use by some teachers really just makes the math (grade calculation) more of an algebra problem - which will automatically terrify and confuse too many of us.
Regardless, I am still trying to understand how adding 20 more (points) to the numerator while the denominator remains unchanged will ever reduce the result (of the category). Maybe the total equation can still result in a very unexpected solution (or the categorization has made the equation too difficult to be properly written by the teacher), but I have to ask.